2024年3月20日,复旦大学林伟教授、朱群喜博士研究团队提出了一种基于格兰杰因果和储备池计算的轻量化机器学习框架,旨在高效且稳健地揭示系统高阶相互作用,并利用这些高阶结构信息进行精准动力学预测。这一研究成果以“Higher-order Granger reservoir computing: Simultaneously achieving scalable complex structures inference and accurate dynamics prediction”为题,在《自然通讯》杂志上发表,并选为应用物理与数学方向的featured article。国际知名学术网站techxplore.com以“Lightweight machine learning method enhances scalable structural inference and dynamic prediction accuracy”为题专文推送了该研究的介绍。

近年来,包括储备池计算(Reservoir Computing, RC)在内的机器学习技术在复杂系统演化预测研究中取得了巨大成功。研究者致力于开发先进的机器学习方法并应用于由复杂系统生成的可观测时间序列数据,旨在深入理解和精准预测系统动力学演化行为。尽管如此,如何在保持模型轻量化的同时,更全面地利用结构信息实现对复杂动力学的精确预测,仍是一个巨大挑战。
实际复杂系统维度之高且动力学行为之复杂,往往超出想象,这是因为系统包含各式各样的非线性高阶交互作用,但这些高阶结构信息一般是仅部分已知甚至完全未知的。因此,如何根据观测的时间序列数据,准确地推断底层的高阶结构信息,是另一个巨大挑战。
为了应对以上两个挑战,研究团队基于格兰杰因果和储备池计算提出了一种数据驱动、无模型的新型机器学习框架,高阶格兰杰储备池计算(Higher-Order Granger RC, HoGRC)(如图1所示)。这一框架的创新之处在于两个核心理念:构建高阶RC并进行动力学预测,以及借助格兰杰因果思想进行高阶结构推断。具体而言,研究团队首先引入了一种节点级别的新计算范式,称为高阶RC。如图1a-b所示,对于任意节点![]() ,高阶RC旨在将结构信息,特别是高阶结构信息通过输入矩
,高阶RC旨在将结构信息,特别是高阶结构信息通过输入矩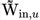 和邻接矩
和邻接矩![]() 编码到储备池计算中。然而,在现实应用中,系统的高阶结构往往部分未知或完全未知。针对这一问题,研究团队利用格兰杰因果的思想,设计了一种贪心迭代算法,用于推断任意节点
编码到储备池计算中。然而,在现实应用中,系统的高阶结构往往部分未知或完全未知。针对这一问题,研究团队利用格兰杰因果的思想,设计了一种贪心迭代算法,用于推断任意节点![]() 的高阶结构,这一过程通过图1a-c的示意图进行了说明。基于这些推断出的高阶结构,研究团队进一步将其编码到高阶RC中,实现了系统演化动力学精准预测,如图1d所示。值得注意的是,HoGRC框架具备良好的可拓展性,可以并行实现结构推断和动力学预测两项任务。
的高阶结构,这一过程通过图1a-c的示意图进行了说明。基于这些推断出的高阶结构,研究团队进一步将其编码到高阶RC中,实现了系统演化动力学精准预测,如图1d所示。值得注意的是,HoGRC框架具备良好的可拓展性,可以并行实现结构推断和动力学预测两项任务。
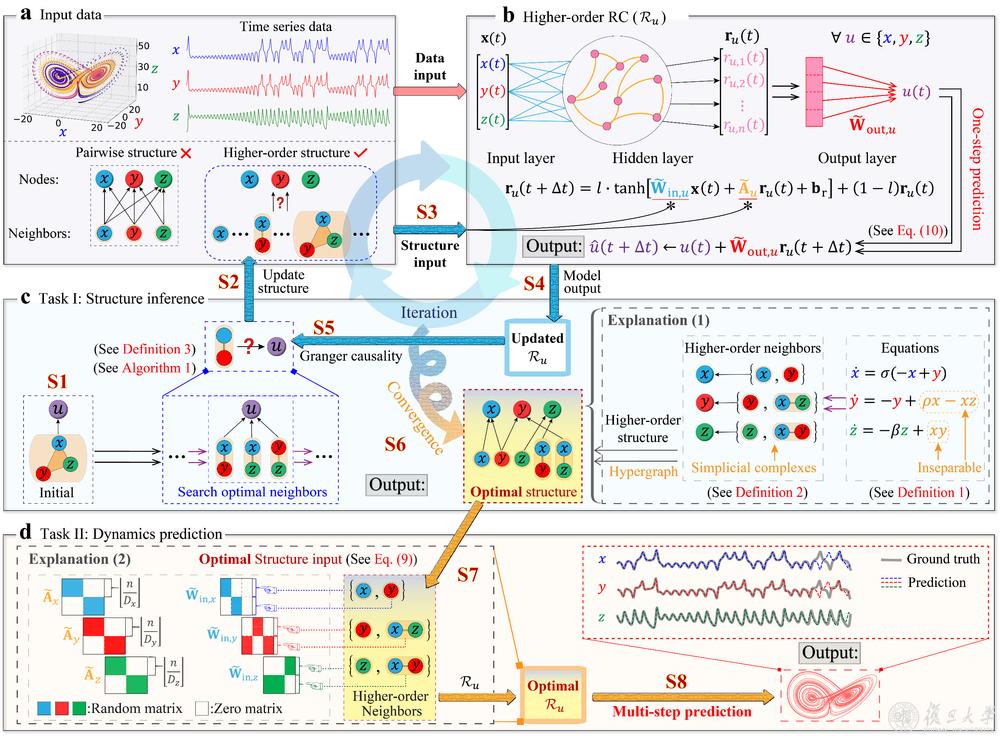
图1:HoGRC框架的示意图。a 观测时间序列和高阶结构作为模型输入数据。b 高阶RC新计算范式。c 高阶结构推断。d 基于推断的高阶结构的演化动力学预测
为了评估HoGRC框架的有效性,研究团队在多种不同领域的系统上进行了测试。首先,在洛伦兹系统这一较为简单的案例中,通过图2a详细展示了使用贪心算法来推断节点![]() 高阶邻居的过程,并且所推断出的最优结构与实际高阶邻居完全吻合。此外,团队还考虑了一个更高维的耦合洛伦兹系统,并在图2b中呈现了其耦合结构。类似的,研究团队基于格兰杰因果的思想在图2c中展示了耦合网络的推断过程,其中包含五个子图,分别表示子系统A-E在不同耦合邻居下的预测误差,进而推断出真实的耦合网络(用红色五角星标记了最优的耦合邻居)。最后,研究团队将经典RC方法和利用成对结构的PRC方法作为基线方法,并在图2d-e中展示了RC, PRC和HoGRC方法在不同耦合项情况下的预测表现。不难发现HoGRC框架相较于基线方法具有更强的预测性能。
高阶邻居的过程,并且所推断出的最优结构与实际高阶邻居完全吻合。此外,团队还考虑了一个更高维的耦合洛伦兹系统,并在图2b中呈现了其耦合结构。类似的,研究团队基于格兰杰因果的思想在图2c中展示了耦合网络的推断过程,其中包含五个子图,分别表示子系统A-E在不同耦合邻居下的预测误差,进而推断出真实的耦合网络(用红色五角星标记了最优的耦合邻居)。最后,研究团队将经典RC方法和利用成对结构的PRC方法作为基线方法,并在图2d-e中展示了RC, PRC和HoGRC方法在不同耦合项情况下的预测表现。不难发现HoGRC框架相较于基线方法具有更强的预测性能。

图2:洛伦兹系统和耦合洛伦兹系统中的实验结果。a 使用贪心算法推断洛伦兹系统中变量![]() 的高阶邻居。b 耦合洛伦兹系统的底层耦合网络。c 在耦合洛伦兹系统中,对每个子系统推断其耦合邻居。d,e RC, PRC和HoGRC方法在不同耦合项情况下的预测表现。其中框图中间的橙色水平线代表中位数,框图的上下边界分别代表上四分位数和下四分位数,上下须的边界分别代表最大值和最小值。
的高阶邻居。b 耦合洛伦兹系统的底层耦合网络。c 在耦合洛伦兹系统中,对每个子系统推断其耦合邻居。d,e RC, PRC和HoGRC方法在不同耦合项情况下的预测表现。其中框图中间的橙色水平线代表中位数,框图的上下边界分别代表上四分位数和下四分位数,上下须的边界分别代表最大值和最小值。
此外,研究团队在其他多种经典混沌系统、网络系统以及英国电网等系统上进行了一系列实验,在结构推断和动力学预测方面均展示了卓越成效。以英国电网系统为例,该系统由120个节点构成(包括10个发电站和110个终端用户),以及165条无向边,其结构如图3a中所示。为了精确模拟电网动力学,研究团队采用了包含高阶交互的Kuramoto模型进行实验,其中图3a中的三角形结构代表了高阶交互项。为了展示HoGRC框架在结构推断上的优势,研究团队特别选取了节点33作为例子,通过贪心算法进行了详细的推断实验,推断过程如图3c所示。可以明显看到,推断结果与图3b中显示的真实高阶结构完全一致。进一步地,图3d和3e分别展示了采用不同预测方法时的平均预测步长和节点33状态预测曲线的比较。可以观察到,HoGRC框架在动力学预测方面比基准方法具有明显的优势。这主要得益于HoGRC框架能够整合系统的高阶结构信息,进而更准确地揭示了系统的底层动力学特性。
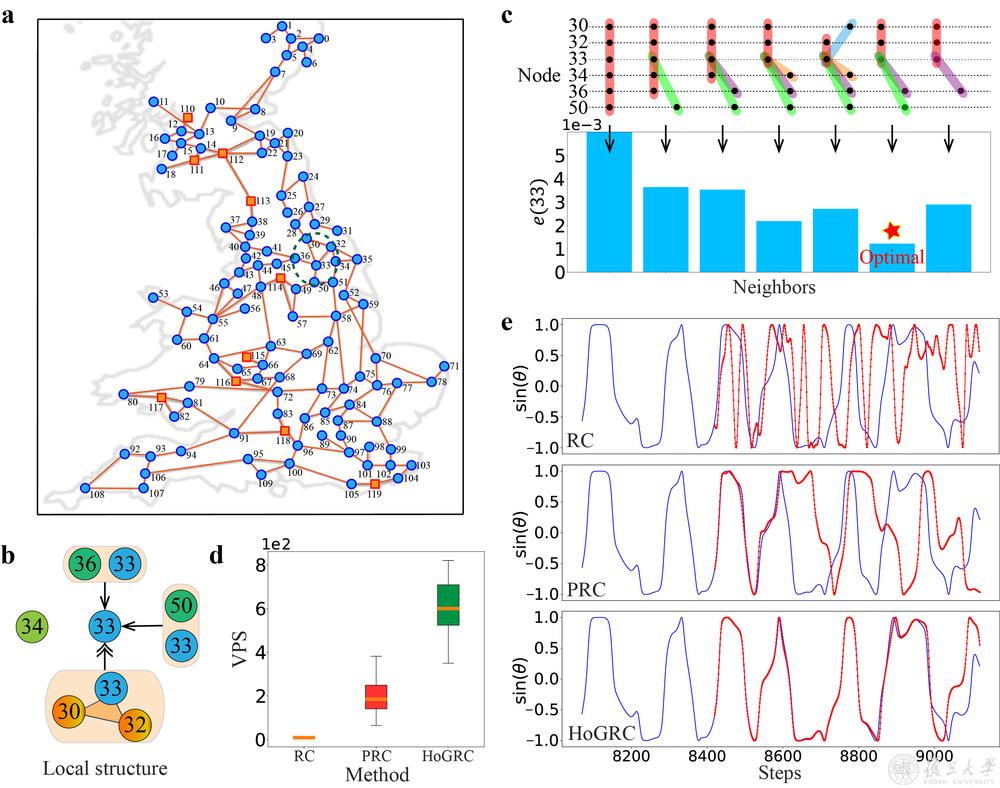
图3:英国电网系统高阶结构推断和动力学预测。a 英国电网结构。b 节点33的高阶结构。c 节点33的高阶邻居推断过程。d RC, PRC和HoGRC方法对整个系统的平均可预测步数,箱线图含义同图2d。e RC, PRC和HoGRC方法对节点33的外推预测表现,其中蓝线表示真实值,红线表示预测值。
在未来的研究中,若干研究方向值得深入研究。特别是,将HoGRC框架应用于更为广泛的复杂系统,尤其是那些涉及更为复杂的高阶交互作用的真实系统,具有重要实际应用价值。进一步,开发一套更加实用的算法以有效减弱或消除间接因果效应亦显得至关重要。此外,建立该框架在泛化能力方面的一般化理论,以及开发基于HoGRC框架概念的新型机器学习框架,都将对机器学习和复杂系统研究领域产生深远影响。总体而言,这些未来的研究方向不仅能推进对复杂系统的深入认识,还将提升HoGRC框架的扩展性、性能、鲁棒性和实际应用价值。
复旦大学智能复杂体系基础理论与关键技术实验室联合培养的国科大博士生李鑫为该论文第一作者,实验室教授林伟、博士朱群喜和国科大副教授赵城利为本文共同通讯作者,苏州大学教授马欢飞也在工作中给予了指导和支持。本研究得到了中国博士后科学基金、上海市超级博士后计划、上海市启明星杨帆专项计划以及上海市科学技术委员会、国家自然科学基金委、上海人工智能实验室、CFFF计算平台的支持。
论文链接:https://doi.org/10.1038/s41467-024-46852-1
报道链接:https://techxplore.com/news/2024-03-lightweight-machine-method-scalable-inference.html





